Over the years, Bootlin has grown a significant expertise in U-Boot and Linux support for flash memory devices. Thanks to this expertise, we have recently been in charge of rewriting and upstreaming a driver for the Arasan NAND controller, which is used in a number of Xilinx Zynq SoCs. It turned out that supporting this NAND controller had some interesting challenges to handle its ECC engine peculiarities. In this blog post, we would like to give some background about ECC issues with NAND flash devices, and then dive into the specific issues that we encountered with the Arasan NAND controller, and how we solved them.
Ensuring data integrity
NAND flash memories are known to be intrinsically rather unstable: over time, external conditions or repetitive access to a NAND device may result in the data being corrupted. This is particularly true with newer chips, where the number of corruptions usually increases with density, requiring even stronger corrections. To mitigate this, Error Correcting Codes are typically used to detect and correct such corruptions, and since the calculations related to ECC detection and correction are quite intensive, NAND controllers often embed a dedicated engine, the ECC engine, to offload those operations from the CPU.
An ECC engine typically acts as a DMA master, moving, correcting data and calculating syndromes on the fly between the controller FIFO’s and the user buffer. The engine correction is characterized by two inputs: the size of the data chunks on which the correction applies and the strength of the correction. Old SLC (Single Level Cell) NAND chips typically require a strength of 1 symbol over 4096 (1 bit/512 bytes) while new ones may require much more: 8, 16 or even 24 symbols.
In the write path, the ECC engine reads a user buffer and computes a code for each chunk of data. NAND pages being longer than officially advertised, there is a persistent Out-Of-Band (OOB) area which may be used to store these codes. When reading data, the ECC engine gets fed by the data coming from the NAND bus, including the OOB area. Chunk by chunk, the engine will do some math and correct the data if needed, and then report the number of corrected symbols. If the number of error is higher than the chosen strength, the engine is not capable of any correction and returns an error.
The Arasan ECC engine
As explained in our introduction, as part of our work on upstreaming the Arasan NAND controller driver, we discovered that this NAND controller IP has a specific behavior in terms of how it reports ECC results: the hardware ECC engine never reports errors. It means the data may be corrected or uncorrectable: the engine behaves the same. From a software point of view, this is a critical flaw and fully relying on such hardware was not an option.
To overcome this limitation, we investigated different solutions, which we detail in the sections below.
Suppose there will never be any uncorrectable error
Let’s be honest, this hypothesis is highly unreliable. Besides that anyway, it would imply that we do not differentiate between written/erased pages and users would receive unclean buffers (with bitflips), which would not work with upper layers such as UBI/UBIFS which expect clean data.
Keep an history of bitflips of every page
This way, during a read, it would be possible to compare the evolution of the number of bitflips. If it suddenly drops significantly, the engine is lying and we are facing an error. Unfortunately it is not a reliable solution either because we should either trigger a write operation every time a read happens (slowing down a lot the I/Os and wearing out very quickly the storage device) or loose the tracking after every power cycle which would make this solution very fragile.
Add a CRC16
This CRC16 could lay in the OOB area and help to manually verify the data integrity after the engine’s correction by checking it against the checksum. This could be acceptable, even if not perfect in term of collisions. However, it would not work with existing data while there are many downstreams users of the vendor driver already.
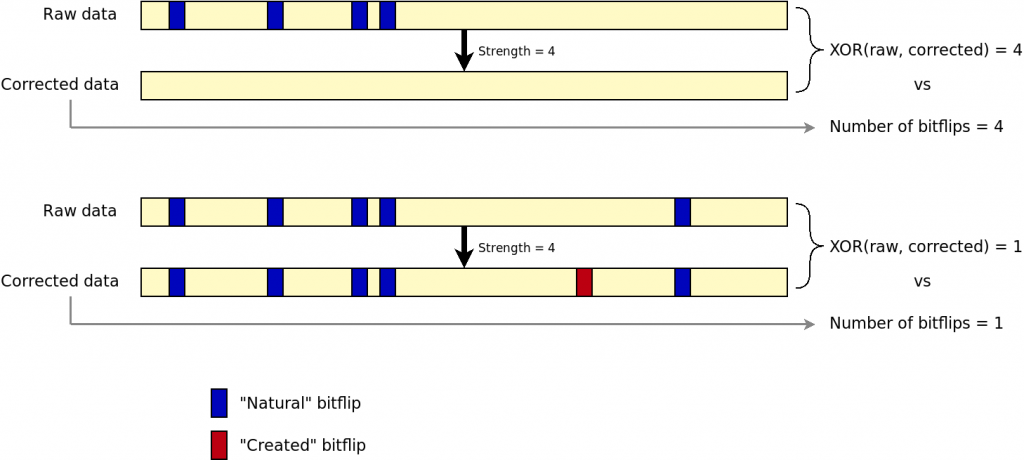
Use a bitwise XOR between raw and corrected data
By doing a bitwise XOR between raw and corrected datra, and compare with the number of bitflips reported by the engine, we could detect if the engine is lying on the number of corrected bitflips. This solution has actually been implemented and tested. It involves extra I/Os as the page must be read twice: first with correction and then again without correction. Hence, the NAND bus throughput becomes a limiting factor. In addition, when there are too many bitflips, the engine still tries to correct data and creates bitflips by itself. The result is that, with just a XOR, we cannot discriminate a working correction from a failure. The following figure shows the issue.
Rely on the hardware only in the write path
Using the hardware engine in the write path is fine (and possibly the quickest solution). Instead of trying to workaround the flaws of the read path, we can do the math by software to derive the syndrome in the read path and compare it with the one in the OOB section. If it does not match, it means we are facing an uncorrectable error. This is finally the solution that we have chosen. Of course, if we want to compare software and hardware calculated ECC bytes, we must find a way to reproduce the hardware calculations, and this is what we are going to explore in the next sections.
Reversing a hardware BCH ECC engine
There is already a BCH library in the Linux kernel on which we could rely on to compute BCH codes. What needed to be identified though, were the BCH initial parameters. In particular:
- The BCH primary polynomial, from which is derived the generator polynomial. The latter is then used for the computation of BCH codes.
- The range of data on which the derivation would apply.
There are several thousands possible primary polynomials with a form like x^3 + x^2 + 1. In order to represent these polynomials more easily by software, we use integers or binary arrays. In both cases, each bit represents the coefficient for the order of magnitude corresponding to its position. The above example could be represented by b1101 or 0xD.
For a given desired BCH code (ie. the ECC chunk size and hence its corresponding Gallois Field order), there is a limited range of possible primary polynomials which can be used. Given eccsize being the amount of data to protect, the Gallois Field order is the smallest integer m so that: 2^m > eccsize. Knowing m, one can check these tables to see examples of polynomials which could match (non exhaustive). The Arasan ECC engine supporting two possible ECC chunk sizes of 512 and 1024 bytes, we had to look at the tables for m = 13 and m = 14.
Given the required strength t, the number of needed parity bits p is: p = t x m.
The total amount of manipulated data (ECC chunk, parity bits, eventual padding) n, also called BCH codeword in papers, is: n = 2^m - 1.
Given the size of the codeword n and the number of parity bits p, it is then possible to derive the maximum message length k with: k = n - p.
The theory of BCH also shows that if (n, k) is a valid BCH code, then (n - x, k - x) will also be valid. In our situation this is very interesting. Indeed, we want to protect eccsize number of symbols, but we currently cover k within n. In other words we could use the translation factor x being: x = k - eccsize. If the ECC engine was also protecting some part of the OOB area, x should have been extended a little bit to match the extra range.
With all this theory in mind, we used GNU Octave to brute force the BCH polynomials used by the Arasan ECC engine with the following logic:
- Write a NAND page with a
eccsize-long ECC step full of zeros, and another one full of ones: this is our known set of inputs.
- Extract each BCH code of
p bits produced by the hardware: this is our known set of outputs.
For each possible primary polynomial with the Gallois Field order m, we derive a generator polynomial, use it to encode both input buffers thanks to a regular BCH derivation, and compare the output syndromes with the expected output buffers.
Because the GNU Octave program was not tricky to write, we first tried to match with the output of Linux software BCH engine. Linux using by default the primary polynomial which is the first in GNU Octave’s list for the desired field order, it was quite easy to verify the algorithm worked.
As unfortunate as it sounds, running this test with the hardware data did not gave any match. Looking more in depth, we realized that visually, there was something like a matching pattern between the output of the Arasan engine and the output of Linux software BCH engine. In fact, both syndromes where identical, the bits being swapped at byte level by the hardware. This observation was made possible because the input buffers have the same values no matter the bit ordering. By extension, we also figured that swapping the bits in the input buffer was also necessary.
The primary polynomial for an eccsize of 512 bytes being already found, we ran again the program with eccsize being 1024 bytes:
eccsize = 1024
eccstrength = 24
m = 14
n = 16383
p = 336
k = 16047
x = 7855
Trying primary polynomial #1: 0x402b
Trying primary polynomial #2: 0x4039
Trying primary polynomial #3: 0x4053
Trying primary polynomial #4: 0x405f
Trying primary polynomial #5: 0x407b
[...]
Trying primary polynomial #44: 0x43c9
Trying primary polynomial #45: 0x43eb
Trying primary polynomial #46: 0x43ed
Trying primary polynomial #47: 0x440b
Trying primary polynomial #48: 0x4443
Primary polynomial found! 0x4443
Final solution
With the two possible primary polynomials in hand, we could finish the support for this ECC engine.
At first, we tried a “mixed-mode” solution: read and correct the data with the hardware engine and then re-read the data in raw mode. Calculate the syndrome over the raw data, derive the number of roots of the syndrome which represents the number of bitflips and compare with the hardware engine’s output. As finding the syndrome’s roots location (ie. the bitflips offsets) is very time consuming for the machine it was decided not to do it in order to gain some time. This approach worked, but doing the I/Os twice was slowing down very much the read speed, much more than expected.
The final approach has been to actually get rid of any hardware computation in the read path, delegating all the work to Linux BCH logic, which indeed worked noticeably faster.
The overall work is now in the upstream Linux kernel:
If you’re interested about more details on ECC for flash devices, and their support in Linux, we will be giving a talk precisely on this topic at the upcoming Embedded Linux Conference!